Cross-platform high-precision decimal arithmetic type. More...

#include <array>
#include <compare>
#include <cstdint>
#include <limits>
#include <optional>
#include <string>
#include <string_view>
#include "Int128.h"
#include "nfx/detail/datatypes/Decimal.inl"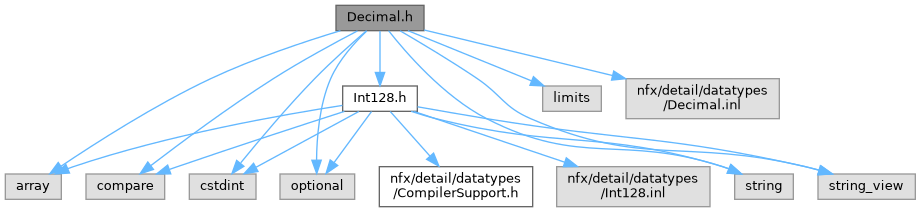

Include dependency graph for Decimal.h:

This graph shows which files directly or indirectly include this file:

Go to the source code of this file.

Classes
class	nfx::datatypes::Decimal
	Cross-platform high-precision decimal type. More...

Functions
Decimal	nfx::datatypes::abs (const Decimal &value) noexcept
	Get absolute value of decimal (free function).
Decimal	nfx::datatypes::sqrt (const Decimal &value)
	Compute square root using Newton-Raphson method (free function).
Decimal	nfx::datatypes::ceil (const Decimal &value) noexcept
	Round up to nearest integer (free function).
Decimal	nfx::datatypes::floor (const Decimal &value) noexcept
	Round down to nearest integer (free function).
Decimal	nfx::datatypes::round (const Decimal &value, std::int32_t decimalsPlacesCount=0, Decimal::RoundingMode mode=Decimal::RoundingMode::ToNearest) noexcept
	Round decimal to specified precision (free function).
Decimal	nfx::datatypes::trunc (const Decimal &value) noexcept
	Remove fractional part (free function).

Detailed Description

Cross-platform high-precision decimal arithmetic type.

Implements the Decimal data type with exact decimal arithmetic and no floating-point rounding errors.

     Range and Precision:
     - Values from -79,228,162,514,264,337,593,543,950,335 to +79,228,162,514,264,337,593,543,950,335
     - 28 significant decimal digits maximum
     - Finite set of values of the form m / 10^e where:
       * m is an integer such that -2^96 < m < 2^96
       * e is an integer between 0 and 28 inclusive

     Key Benefits:
     - Exact representation of decimal fractions (e.g., 0.1 is represented exactly)
     - No round-off errors in financial calculations
     - Ideally suited for monetary and high-precision decimal arithmetic

     Storage Format:
     - 96-bit mantissa + 32-bit scale/sign = 128-bit total storage

     Memory Layout of Decimal (128 bits / 16 bytes):
     ==============================================

     1. Flags (32 bits):
     ┌───────────┬─────────────────────────────────────┬───────────────────────────────────────────────────┐
     │    Bits   │             Description             │                       Notes                       │
     ├───────────┼─────────────────────────────────────┼───────────────────────────────────────────────────┤
     │   0 - 15  │  Unused (must be zero)              │  Reserved - Required to be zero for valid format  │
     │  16 - 23  │  Scale (0-28)                       │  Number of decimal digits after decimal point     │
     │  24 - 30  │  Unused (must be zero)              │  Reserved - Required to be zero for valid format  │
     │  31       │  Sign (0 = positive, 1 = negative)  │  Sign bit                                         │
     └───────────┴─────────────────────────────────────┴───────────────────────────────────────────────────┘

     2. Mantissa (96 bits total):
     ┌───────────────┬───────────┬─────────────────────────────────┐
     │ Mantissa Part │   Bits    │           Description           │
     ├───────────────┼───────────┼─────────────────────────────────┤
     │  mantissa[0]  │   0 - 31  │  Lower 32 bits of the mantissa  │
     │  mantissa[1]  │  32 - 63  │  Middle 32 bits of the mantissa │
     │  mantissa[2]  │  64 - 95  │  Upper 32 bits of the mantissa  │
     └───────────────┴───────────┴─────────────────────────────────┘

     Complete Memory Layout (128 bits / 16 bytes):
     =============================================

     ┌─────────────────────────────────┬─────────────────────────────────┬─────────────────────────────────┬─────────────────────────────────┐
     │         mantissa[2]             │         mantissa[1]             │          mantissa[0]            │            flags                │
     │       (upper 32 bits)           │      (middle 32 bits)           │       (lower 32 bits)           │        (scale + sign)           │
     │          32 bits                │          32 bits                │           32 bits               │            32 bit               │
     └─────────────────────────────────┴─────────────────────────────────┴─────────────────────────────────┴─────────────────────────────────┘
     Bit 127                     Bit 96 Bit 95                     Bit 64 Bit 63                     Bit 32 Bit 31                       Bit 0

     Where the 96-bit mantissa represents an unsigned integer from 0 to 2^96-1
     and the sign is stored separately in bit 31 of the flags word.

     Summary:
     =======

     - Total storage: 128 bits (16 bytes)
     - Value formula: decimal_value = mantissa / 10^scale × (sign ? -1 : 1)

     Examples with Memory Layout:
     ============================

     Example 1 - Value 123.45:
     - mantissa: 12345 (stored across mantissa[0-2])
     - scale   : 2 (bits 16-23 of flags, 2 decimal places)
     - sign    : 0 (bit 31 of flags, positive)
     - result  : 12345 / 10² = 123.45

     Example 2 - Value -12,345,678,901,234,567,890.123456789:
     - mantissa: 12345678901234567890123456789 (96-bit value across mantissa[0-2])
                 mantissa[0] = 0x15CD5B07  - 365,072,135   (lower 32 bits)
                 mantissa[1] = 0x9CE5A30A  - 2,632,713,994 (middle 32 bits)
                 mantissa[2] = 0x27B95E997 - 669,260,439   (upper 32 bits)
     - scale   : 9 (bits 16-23 of flags, 9 decimal places)
     - sign    : 1 (bit 31 of flags, negative)
     - result  : 12345678901234567890123456789 / 10⁹ × (-1) = -12,345,678,901,234,567,890.123456789

     - Original = (mantissa[2] × 2^64) + (mantissa[1] × 2^32) + mantissa[0]
     - Original = (669,260,439 × 18,446,744,073,709,551,616) + (2,632,713,994 × 4,294,967,296) + 365,072,135
     - Original = 12345678901234567890123456789

     IEEE 754-2008 binary64 Input Compatibility:
     - Construction from double uses IEEE 754-2008 std::isnan and std::isinf functions
     - Preserves IEEE 754 binary64 precision limits (~15-17 digits)
     - NaN and Infinity from double are converted to zero
     - String construction provides exact decimal precision (up to 28 digits)

Note: This is NOT IEEE 754 decimal128 arithmetic - it implements exact fixed-point decimal arithmetic without floating-point rounding errors.; Design inspired by .NET System.Decimal semantics (96-bit mantissa + scale, 28–29 digits, banker's rounding).

Definition in file Decimal.h.

Function Documentation

◆ abs()

Decimal nfx::datatypes::abs ( const Decimal & value )

inlinenodiscardnoexcept

Get absolute value of decimal (free function).

Parameters

value Decimal to get absolute value of

Returns: Absolute value of the decimal

Free function wrapper for generic programming and ADL (Argument-Dependent Lookup). Enables usage in generic algorithms: sqrt(value) works via ADL.

Note: This function is marked [[nodiscard]] - the return value should not be ignored

Definition at line 894 of file Decimal.h.

◆ ceil()

Decimal nfx::datatypes::ceil ( const Decimal & value )

inlinenodiscardnoexcept

Round up to nearest integer (free function).

Parameters

value Decimal to ceiling

Returns: Smallest integer greater than or equal to value

Free function wrapper for generic programming and ADL (Argument-Dependent Lookup).

Note: This function is marked [[nodiscard]] - the return value should not be ignored

Definition at line 920 of file Decimal.h.

◆ floor()

Decimal nfx::datatypes::floor ( const Decimal & value )

inlinenodiscardnoexcept

Round down to nearest integer (free function).

Parameters

value Decimal to floor

Returns: Largest integer less than or equal to value

Free function wrapper for generic programming and ADL (Argument-Dependent Lookup).

Note: This function is marked [[nodiscard]] - the return value should not be ignored

Definition at line 932 of file Decimal.h.

◆ round()

Decimal nfx::datatypes::round	(	const Decimal &	value,
		std::int32_t	decimalsPlacesCount = 0,
		Decimal::RoundingMode	mode = Decimal::RoundingMode::ToNearest )

inlinenodiscardnoexcept

Round decimal to specified precision (free function).

Parameters

value	Decimal value to round
decimalsPlacesCount	Number of decimal places to round to (default: 0)
mode	Rounding mode to apply (default: RoundingMode::ToNearest)

Returns: Decimal value rounded to the specified precision

Free function wrapper for generic programming and ADL (Argument-Dependent Lookup). Enables usage in generic algorithms.

Note: This function is marked [[nodiscard]] - the return value should not be ignored

Definition at line 947 of file Decimal.h.

◆ sqrt()

Decimal nfx::datatypes::sqrt ( const Decimal & value )

inlinenodiscard

Compute square root using Newton-Raphson method (free function).

Parameters

value Decimal to compute square root of

Returns: Square root with full decimal precision (up to 28 digits)

Exceptions

std::domain_error if called on negative value

Free function wrapper for generic programming and ADL (Argument-Dependent Lookup). Enables usage in generic algorithms: sqrt(value) works via ADL.

Note: This function is marked [[nodiscard]] - the return value should not be ignored

Definition at line 908 of file Decimal.h.

Here is the call graph for this function:

◆ trunc()

Decimal nfx::datatypes::trunc ( const Decimal & value )

inlinenodiscardnoexcept

Remove fractional part (free function).

Parameters

value Decimal to truncate

Returns: Decimal with fractional part removed

Free function wrapper for generic programming and ADL (Argument-Dependent Lookup).

Note: This function is marked [[nodiscard]] - the return value should not be ignored

Definition at line 960 of file Decimal.h.

Classes

Functions

Detailed Description

Function Documentation

◆ abs()

◆ ceil()

◆ floor()

◆ round()

◆ sqrt()

◆ trunc()